Proprietà della funzione esponenziale. Lezione “Funzione esponenziale, sue proprietà e grafico
Funzione esponenziale
Funzione della forma y = a X , dove a è maggiore di zero e a non è uguale a uno è detta funzione esponenziale. Proprietà di base della funzione esponenziale:
1. Il dominio di definizione della funzione esponenziale sarà l'insieme dei numeri reali.
2. L'intervallo di valori della funzione esponenziale sarà l'insieme di tutti i numeri reali positivi. A volte questo insieme è indicato come R+ per brevità.
3. Se in una funzione esponenziale la base a è maggiore di uno, la funzione sarà crescente nell'intero dominio di definizione. Se nella funzione esponenziale per la base a è soddisfatta la seguente condizione 0
4. Tutte le proprietà di base dei titoli di studio saranno valide. Le principali proprietà dei gradi sono rappresentate dalle seguenti uguaglianze:
UN X *UN sì = un (x+y) ;
(UN X )/(UN sì ) = a (xy) ;
(a*b) X = (a X )*(UN sì );
(a/b) X = un X /B X ;
(UN X ) sì = un (x*y) .
Queste uguaglianze saranno valide per tutti i valori reali di x e y.
5. Il grafico di una funzione esponenziale passa sempre per il punto di coordinate (0;1)
6. A seconda che la funzione esponenziale aumenti o diminuisca, il suo grafico avrà due forme.
La figura seguente mostra il grafico di una funzione esponenziale crescente: a>0.
La figura seguente mostra il grafico di una funzione esponenziale decrescente: 0

Sia il grafico di una funzione esponenziale crescente che il grafico di una funzione esponenziale decrescente, secondo la proprietà descritta nel quinto paragrafo, passano per il punto (0;1).
7. Una funzione esponenziale non ha punti estremi, cioè non ha punti minimo e massimo della funzione. Se consideriamo una funzione su un segmento specifico, la funzione assumerà i valori minimo e massimo alle estremità di questo intervallo.
8. La funzione non è né pari né dispari. Una funzione esponenziale è una funzione di forma generale. Lo si vede dai grafici; nessuno di essi è simmetrico né rispetto all'asse Oy né rispetto all'origine delle coordinate.
Logaritmo

I logaritmi sono sempre stati considerati un argomento difficile nei corsi di matematica scolastica. Esistono molte definizioni diverse di logaritmo, ma per qualche motivo la maggior parte dei libri di testo utilizza quelle più complesse e infruttuose.
Definiremo il logaritmo in modo semplice e chiaro. Per fare ciò, creiamo una tabella:
Quindi abbiamo potenze di due. Se prendi il numero dalla riga inferiore, puoi facilmente trovare la potenza alla quale dovrai alzare due per ottenere questo numero. Ad esempio, per ottenere 16, devi elevare due alla quarta potenza. E per ottenere 64, devi elevare due alla sesta potenza. Questo può essere visto dalla tabella.
E ora, in realtà, la definizione del logaritmo:
Definizione
Logaritmo per basare a sull'argomento x è la potenza alla quale il numero deve essere elevato UN per ottenere il numero X.
Designazione
logaritmo a x = b
dove a è la base, x è l'argomento, b - in realtà, a cosa equivale il logaritmo.
Ad esempio, 2 3 = 8 ⇒ log 2 8 = 3 (il logaritmo in base 2 di 8 è tre perché 2 3 = 8). Con lo stesso successo, log 2 64 = 6, poiché 2 6 = 64.
Si chiama l'operazione di trovare il logaritmo di un numero in una data baselogaritmo . Quindi, aggiungiamo una nuova riga alla nostra tabella:
Sfortunatamente, non tutti i logaritmi si calcolano così facilmente. Ad esempio, prova a trovare log 2 5. Il numero 5 non è nella tabella, ma la logica impone che il logaritmo si trovi da qualche parte nell'intervallo. Perché 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Tali numeri sono detti irrazionali: i numeri dopo la virgola possono essere scritti all'infinito e non si ripetono mai. Se il logaritmo risulta irrazionale, è meglio lasciarlo così: log 2 5, log 3 8, log 5 100.
È importante capire che un logaritmo è un'espressione con due variabili (la base e l'argomento). Inizialmente, molte persone confondono dove sia la base e dove sia l’argomento. Per evitare fastidiosi malintesi basta guardare l'immagine:
Davanti a noi non c'è altro che la definizione di logaritmo. Ricorda: il logaritmo è una potenza , in cui è necessario costruire la base per ottenere un argomento.È la base che viene elevata a potenza: nell'immagine è evidenziata in rosso. Si scopre che la base è sempre in basso! Dico ai miei studenti questa meravigliosa regola già dalla prima lezione e non si crea alcuna confusione.
Abbiamo capito la definizione: non resta che imparare a contare i logaritmi, ad es. sbarazzarsi del segno "log". Per cominciare, lo notiamo Dalla definizione conseguono due fatti importanti:
L'argomento e la base devono essere sempre maggiori di zero. Ciò deriva dalla definizione di grado mediante esponente razionale, a cui si riduce la definizione di logaritmo.
La base deve essere diversa da uno, poiché uno in ogni grado rimane pur sempre uno. Per questo motivo la domanda “a quale potere bisogna elevare uno per averne due” non ha senso. Non esiste un diploma del genere!
Tali restrizioni sono chiamati intervallo di valori accettabili(ODZ). Risulta che l'ODZ del logaritmo assomiglia a questo: log un x = b ⇒ x > 0, a > 0, a ≠ 1.
Tienilo presente nessuna restrizione sul numero B (valore logaritmo) non si sovrappone. Ad esempio, il logaritmo potrebbe essere negativo: log 2 0,5 = −1, perché 0,5 = 2 −1.
Tuttavia, ora consideriamo solo espressioni numeriche, dove non è necessario conoscere il VA del logaritmo. Tutte le restrizioni sono già state prese in considerazione dagli autori dei problemi. Ma quando entrano in gioco le equazioni e le disuguaglianze logaritmiche, i requisiti DL diventeranno obbligatori. Dopotutto, la base e l'argomentazione possono contenere costruzioni molto forti che non corrispondono necessariamente alle restrizioni di cui sopra.
Ora considera il generale schema per il calcolo dei logaritmi. Si compone di tre passaggi:
Fornisci una ragione a e argomento x sotto forma di potenza con la base minima possibile maggiore di uno. Lungo il percorso, è meglio eliminare i decimali;
Risolvere rispetto ad una variabile b equazione: x = a b ;
Il numero risultante b sarà la risposta.
Questo è tutto! Se il logaritmo risultasse irrazionale, ciò sarà visibile già nel primo passaggio. Molto importante è il requisito che la base sia maggiore di uno: questo riduce la probabilità di errore e semplifica moltissimo i calcoli. Con le frazioni decimali è lo stesso: se le converti immediatamente in frazioni ordinarie, ci saranno molti meno errori.
Vediamo come funziona questo schema utilizzando esempi specifici:
Calcola il logaritmo: log 5 25
Immaginiamo la base e l'argomento come una potenza di cinque: 5 = 5 1 ; 25 = 5 2 ;
Creiamo e risolviamo l'equazione:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
Abbiamo ricevuto la risposta: 2.
Calcola il logaritmo:
Immaginiamo la base e l'argomento come una potenza di tre: 3 = 3 1 ; 1/81 = 81 −1 = (3 4) −1 = 3 −4 ;
Creiamo e risolviamo l'equazione:
Abbiamo ricevuto la risposta: −4.
−4
Calcola il logaritmo: log 4 64
Immaginiamo la base e l'argomento come una potenza di due: 4 = 2 2 ; 64 = 2 6 ;
Creiamo e risolviamo l'equazione:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
Abbiamo ricevuto la risposta: 3.
Calcola il logaritmo: log 16 1
Immaginiamo la base e l'argomento come una potenza di due: 16 = 2 4 ; 1 = 2 0 ;
Creiamo e risolviamo l'equazione:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
Abbiamo ricevuto la risposta: 0.
Calcola il logaritmo: log 7 14
Immaginiamo la base e l'argomento come una potenza di sette: 7 = 7 1 ; 14 non può essere rappresentato come una potenza di sette, poiché 7 1< 14 < 7 2 ;
Dal paragrafo precedente ne consegue che il logaritmo non conta;
La risposta è nessun cambiamento: log 7 14.
ceppo7 14
Una piccola nota sull'ultimo esempio. Come puoi essere sicuro che un numero non sia una potenza esatta di un altro numero? È molto semplice: basta fattorizzarlo in fattori primi. Se l'espansione ha almeno due fattori diversi, il numero non è una potenza esatta.
Scopri se i numeri sono potenze esatte: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 - grado esatto, perché c'è un solo moltiplicatore;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - non è una potenza esatta, poiché ci sono due fattori: 3 e 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - grado esatto;
35 = 7 · 5 - ancora una volta non una potenza esatta;
14 = 7 · 2 - ancora una volta non un grado esatto;
8, 81 - grado esatto; 48, 35, 14 - n.
Si noti inoltre che i numeri primi stessi sono sempre potenze esatte di se stessi.
Logaritmo decimale
Alcuni logaritmi sono così comuni che hanno un nome e un simbolo speciali.
Definizione
Logaritmo decimale dall'argomento x è il logaritmo in base 10, cioè la potenza alla quale bisogna elevare il numero 10 per ottenere il numero X.
Designazione
lgx
Ad esempio, log 10 = 1; logaritmo 100 = 2; lg 1000 = 3 - ecc.
D'ora in poi, quando in un libro di testo apparirà una frase come "Trova lg 0.01", sappi che non si tratta di un errore di battitura. Questo è un logaritmo decimale. Tuttavia, se non hai familiarità con questa notazione, puoi sempre riscriverla:
logaritmo x = logaritmo 10 x
Tutto ciò che vale per i logaritmi ordinari vale anche per i logaritmi decimali.
Logaritmo naturale
C'è un altro logaritmo che ha una sua designazione. In un certo senso, è ancora più importante del decimale. Stiamo parlando del logaritmo naturale.
Definizione
Logaritmo naturale dall'argomento x è il logaritmo in base e , cioè. la potenza a cui deve essere elevato un numero e per ottenere il numero X.
Designazione
lnx
Molti si chiederanno: qual è il numero e? Questo è un numero irrazionale; il suo valore esatto non può essere trovato e scritto. Darò solo le prime cifre:
e = 2,718281828459...
Non entreremo nei dettagli su cosa sia questo numero e perché è necessario. Ricorda solo che e - base del logaritmo naturale:
ln x = log e x
Quindi ln e = 1; ln e 2 = 2; ln e 16 = 16 - ecc. D'altra parte, ln 2 è un numero irrazionale. In generale, il logaritmo naturale di qualsiasi numero razionale è irrazionale. Tranne, ovviamente, uno: ln 1 = 0.
Per i logaritmi naturali valgono tutte le regole valide per i logaritmi ordinari.
Proprietà fondamentali dei logaritmi
I logaritmi, come qualsiasi numero, possono essere aggiunti, sottratti e trasformati in ogni modo. Ma poiché i logaritmi non sono esattamente numeri ordinari, hanno le loro regole, chiamate proprietà di base.
Devi assolutamente conoscere queste regole: senza di esse non è possibile risolvere un solo problema logaritmico serio. Inoltre, ce ne sono pochissimi: puoi imparare tutto in un giorno. Quindi cominciamo.
Somma e sottrazione di logaritmi
Consideriamo due logaritmi con le stesse basi: log a x e log a y . Quindi possono essere aggiunti e sottratti e:
tronco d'albero un'x + registro un sì = registro UN ( X · sì );
tronco d'albero un'x − registro un sì = registro UN ( X : sì ).
COSÌ, la somma dei logaritmi è uguale al logaritmo del prodotto e la differenza è uguale al logaritmo del quoziente. Nota: il punto chiave qui sono gli stessi motivi. Se i motivi sono diversi, queste regole non funzionano!
Queste formule ti aiuteranno a calcolare un'espressione logaritmica anche quando le sue singole parti non vengono considerate (vedi lezione " "). Dai un'occhiata agli esempi e vedi:
Trova il valore dell'espressione: log 6 4 + log 6 9.
Poiché i logaritmi hanno le stesse basi, usiamo la formula di somma:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Trova il valore dell'espressione: log 2 48 − log 2 3.
Le basi sono le stesse, usiamo la formula della differenza:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Trova il valore dell'espressione: log 3 135 − log 3 5.
Anche in questo caso le basi sono le stesse, quindi abbiamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Come puoi vedere, le espressioni originali sono composte da logaritmi “cattivi”, che non vengono calcolati separatamente. Ma dopo le trasformazioni si ottengono numeri del tutto normali. Molti test si basano su questo fatto. Sì, le espressioni simili ai test vengono offerte in tutta serietà (a volte praticamente senza modifiche) durante l'Esame di Stato unificato.
Estrarre l'esponente dal logaritmo
Ora complichiamo un po' il compito. Cosa succede se la base o l'argomento di un logaritmo è una potenza? Poi l'esponente di questo grado può essere estratto dal segno del logaritmo secondo le seguenti regole:
È facile vedere che l'ultima regola segue le prime due. Ma è comunque meglio ricordarlo: in alcuni casi ridurrà significativamente la quantità di calcoli.
Ovviamente Tutte queste regole hanno senso se si rispetta l'ODZ del logaritmo: a > 0, a ≠ 1, x > 0. E ancora una cosa: impara ad applicare tutte le formule non solo da sinistra a destra, ma anche viceversa, cioè Puoi inserire i numeri prima del segno del logaritmo nel logaritmo stesso. Questo è ciò che più spesso viene richiesto.
Trova il valore dell'espressione: log 7 49 6 .
Eliminiamo la laurea nell'argomento utilizzando la prima formula:
logaritmo 7 49 6 = 6 logaritmo 7 49 = 6 2 = 12
Trova il significato dell'espressione:
Nota che il denominatore contiene un logaritmo, la cui base e argomento sono potenze esatte: 16 = 2 4 ; 49 = 72. Abbiamo:

Penso che l’ultimo esempio richieda alcuni chiarimenti. Dove sono finiti i logaritmi? Fino all'ultimo momento lavoriamo solo con il denominatore. Abbiamo presentato la base e l'argomento del logaritmo sotto forma di potenze e abbiamo eliminato gli esponenti: abbiamo ottenuto una frazione "a tre piani".
Ora diamo un'occhiata alla frazione principale. Il numeratore e il denominatore contengono lo stesso numero: log 2 7. Poiché log 2 7 ≠ 0, possiamo ridurre la frazione: 2/4 rimarranno nel denominatore. Secondo le regole dell'aritmetica, il quattro può essere trasferito al numeratore, e così è stato fatto. Il risultato è stata la risposta: 2.
Transizione ad una nuova fondazione
Parlando delle regole per aggiungere e sottrarre i logaritmi, ho sottolineato in particolare che funzionano solo con le stesse basi. E se i motivi fossero diversi? E se non fossero potenze esatte dello stesso numero?
Le formule per il passaggio a una nuova fondazione vengono in soccorso. Formuliamoli sotto forma di teorema:
Teorema
Sia dato il logaritmo un'x . Quindi per qualsiasi numero c tale che c > 0 e c ≠ 1, l'uguaglianza è vera:
![]()
In particolare, se mettiamo c = x, otteniamo:
![]()
Dalla seconda formula segue che la base e l'argomento del logaritmo possono essere invertiti, ma in questo caso l'intera espressione viene “capovolta”, cioè il logaritmo appare al denominatore.
Queste formule si trovano raramente nelle comuni espressioni numeriche. È possibile valutare quanto siano convenienti solo quando si risolvono equazioni e disequazioni logaritmiche.
Tuttavia, ci sono problemi che non possono essere risolti se non passando a una nuova fondazione. Diamo un'occhiata ad un paio di questi:
Trova il valore dell'espressione: log 5 16 log 2 25.
Nota che gli argomenti di entrambi i logaritmi contengono potenze esatte. Togliamo gli indicatori: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Adesso “invertiamo” il secondo logaritmo:
Poiché il prodotto non cambia quando si riorganizzano i fattori, abbiamo moltiplicato con calma quattro per due e poi ci siamo occupati dei logaritmi.
Trova il valore dell'espressione: log 9 100 lg 3.
La base e l'argomento del primo logaritmo sono potenze esatte. Scriviamolo ed eliminiamo gli indicatori:
Ora eliminiamo il logaritmo decimale spostandoci su una nuova base:
Identità logaritmica di base
Spesso nel processo risolutivo è necessario rappresentare un numero come logaritmo in base data. In questo caso ci aiuteranno le seguenti formule:
Nel primo caso, il numero N diventa un indicatore del grado di validità dell'argomentazione. Numero N può essere assolutamente qualsiasi cosa, perché è solo un valore logaritmico.
La seconda formula è in realtà una definizione parafrasata. Questo è quello che si chiama:identità logaritmica di base.
Infatti, cosa succede se il numero b viene elevato a una potenza tale che il numero b a questa potenza dà il numero a? Esatto: il risultato è lo stesso numero a. Leggi di nuovo attentamente questo paragrafo: molte persone rimangono bloccate.
Come le formule per passare a una nuova base, l'identità logaritmica di base è talvolta l'unica soluzione possibile.
Compito
Trova il significato dell'espressione:
Soluzione
Si noti che log 25 64 = log 5 8 - Prendeva semplicemente il quadrato dalla base e l'argomento del logaritmo. Tenendo conto delle regole per moltiplicare le potenze con la stessa base, otteniamo:
200
Se qualcuno non lo sa, questo è stato un vero compito dell'Esame di Stato Unificato :)
Unità logaritmica e zero logaritmico
In conclusione, darò due identità che difficilmente possono essere chiamate proprietà, ma piuttosto sono conseguenze della definizione del logaritmo. Compaiono costantemente nei problemi e, sorprendentemente, creano problemi anche agli studenti “avanzati”.
log a a = 1 è unità logaritmica. Ricorda una volta per tutte: logaritmo in base qualsiasi UN da questa stessa base è uguale a uno.
log a 1 = 0 è zero logaritmico. Base A può essere qualsiasi cosa, ma se l'argomento ne contiene uno, il logaritmo è uguale a zero! Perché uno 0 = 1 è una conseguenza diretta della definizione.
Queste sono tutte le proprietà. Assicurati di esercitarti a metterli in pratica!
1. Una funzione esponenziale è una funzione della forma y(x) = a x, dipendente dall'esponente x, con valore costante della base del grado a, dove a > 0, a ≠ 0, xϵR (R è il insieme di numeri reali).
Consideriamo grafico della funzione se la base non soddisfa la condizione: a>0
a)a< 0
Se a< 0 – возможно возведение в целую степень или в рациональную степень с нечетным показателем.
a = -2

Se a = 0, la funzione y = è definita e ha un valore costante pari a 0

c) a =1
Se a = 1, la funzione y = è definita e ha valore costante pari a 1
Dominio della funzione (DOF) Intervallo di valori di funzione consentiti (APV) 3. Zeri della funzione (y = 0) 4. Punti di intersezione con l'asse delle ordinate oy (x = 0) 5. Funzioni crescenti e decrescenti Se , allora la funzione f(x) aumenta 6. Funzione pari, dispari La funzione y= non è simmetrica rispetto all'asse 0y e rispetto all'origine delle coordinate, quindi non è né pari né dispari. (Funzione generale) 7. La funzione y = non ha estremi 8. Proprietà di un grado con esponente reale: Sia a > 0; a≠1 Quindi per xϵR; tuR: Proprietà della monotonia del grado: se, allora Se a> 0, allora . 9. Posizione relativa della funzione Quanto più grande è la base a, tanto più vicina agli assi x e oy a > 1, a = 20 Esempio 1. Introduciamo innanzitutto la definizione di funzione esponenziale. Funzione esponenziale $f\left(x\right)=a^x$, dove $a >1$. Introduciamo le proprietà della funzione esponenziale per $a >1$. \ \[nessuna radice\] \ Intersezione con gli assi coordinati. La funzione non interseca l'asse $Ox$, ma interseca l'asse $Oy$ nel punto $(0,1)$. $f""\sinistra(x\destra)=(\sinistra(a^xlna\destra))"=a^x(ln)^2a$ \ \[nessuna radice\] \ Grafico (Fig. 1). Figura 1. Grafico della funzione $f\left(x\right)=a^x,\for\a >1$. Introduciamo le proprietà della funzione esponenziale, a $0 Il dominio della definizione sono tutti i numeri reali. $f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- la funzione non è né pari né dispari. $f(x)$ è continua nell'intero dominio di definizione. L'intervallo di valori è l'intervallo $(0,+\infty)$. $f"(x)=\sinistra(a^x\destra)"=a^xlna$ \ \[nessuna radice\] \ \[nessuna radice\] \ La funzione è convessa su tutto il dominio di definizione. Comportamento alle estremità del dominio: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\] Grafico (Fig. 2). Esplora e traccia la funzione $y=2^x+3$. Soluzione. Conduciamo uno studio utilizzando il diagramma di esempio sopra: Il dominio della definizione sono tutti i numeri reali. $f\left(-x\right)=2^(-x)+3$ -- la funzione non è né pari né dispari. $f(x)$ è continua nell'intero dominio di definizione. L'intervallo di valori è l'intervallo $(3,+\infty)$. $f"\sinistra(x\destra)=(\sinistra(2^x+3\destra))"=2^xln2>0$ La funzione aumenta lungo l'intero dominio di definizione. $f(x)\ge 0$ in tutto il dominio di definizione. Intersezione con gli assi coordinati. La funzione non interseca l'asse $Ox$, ma interseca l'asse $Oy$ nel punto ($0,4)$ $f""\sinistra(x\destra)=(\sinistra(2^xln2\destra))"=2^x(ln)^22>0$ La funzione è convessa su tutto il dominio di definizione. Comportamento alle estremità del dominio: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\] Grafico (Fig. 3). Figura 3. Grafico della funzione $f\left(x\right)=2^x+3$
2. Diamo uno sguardo più da vicino alla funzione esponenziale:
0


Se , allora la funzione f(x) diminuisce
Funzione y= , a 0
Ciò deriva dalle proprietà di monotonia di una potenza con esponente reale.
b>0; b≠1
Per esempio:


La funzione esponenziale è continua in ogni punto ϵ R.


Se a0, la funzione esponenziale assume una forma vicina a y = 0.
Se a1, allora si allontana dagli assi ox e oy e il grafico assume una forma vicina alla funzione y = 1.
Costruisci un grafico di y =
Funzione esponenziale $f\sinistra(x\destra)=a^x$, dove $0
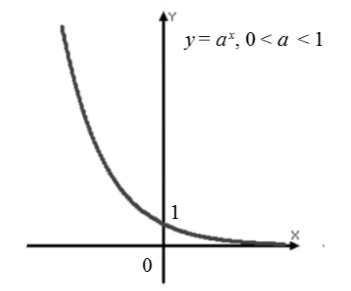
Un esempio di problema per costruire una funzione esponenziale







